Equation of a Progressive Wave

The  distance between two consecutive crests or troughs is called:

Establish the expression for the speed of a progressive wave.

Establish that the particle velocity and the wave velocity of a progressive wave is different.

Select the wrong statement about a progressive wave.

Write the characteristics of a progressive wave

Define wave motion. Write down the characteristics of wave motion.

The equation of a transverse wave travelling along a string is given by $\mathrm{Y}=2.0 \sin \pi (0.2 \mathrm{x}-2.0\mathrm{t})$, where $\mathrm{y},\mathrm{x}$ are in meters and $t$ is in seconds Find the amplitude, wavelength speed and frequency of the wave.

A simple harmonic wave having an amplitude A and time-period T is represented by the equation, $y=5 \sin \pi \left(t+4\right)$ metre. Then, the values of A (in metre) and T (in second) are :

A wave motion has the function $y=a_0\sin \left(\mathrm{\omega }t-kx\right)$. The graph in the figure shows how the displacement $y$ at a fixed point varies with time $t$. Which one of the labelled points shows a displacement equal to that at the position $x=\frac{\mathrm{\pi }}{2k}$ at time $t=0 ?$

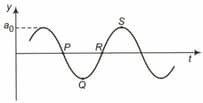
If the speed of the wave shown in the figure is $330 \mathrm{m} {\mathrm{s}}^{-1}$ in the given medium, then the equation of the wave propagating in the positive $x$-direction will be (all quantities are in MKS units)

A harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90 m/s² respectively. Velocity of the wave is 20 m/s. Find the waveform.

State any four characteristics of simple harmonic progressive wave.

Derive an expression for a one dimensional simple harmonic progressive wave travelling in the direction of the positive X-axis. Express it in different forms.

In the above question, the displacement of particle at $t=1 \sec$ and $x=4 \mathrm{cm}$ is 

$Y=5\sin \frac{\pi }{2}\left(100 t-2x\right),$ what is time period?

Two particles ${\text{P}}_1$ and ${\text{P}}_{\text{2}}$ are performing SHM along the same line about the same mean position. Initially, they are in their positive extreme positions. If the time period of each particle is 12 sec and the difference of their amplitudes is 12 cm then find the minimum time after which the separation between them become 6 cm

A transverse wave is represented by the equation $y=2\sin \left(30t-40x\right)$ and the measurement of distance are in meters, then the velocity of propagation is

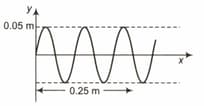
The frequency of the sinusoidal wave $\xi =0.40\cos \left[2000t+0.80\right]$would be

The transvers wave represented by the equation $y=4\sin \left(\frac{\pi }{6}\right)\sin \left(3x-15t\right)$ has

A transverse wave is described by the equation, $\mathrm{y}={\mathrm{y}}_0\sin 2\mathrm{\pi }\left(\mathrm{f}\mathrm{t}-\frac{\mathrm{x}}{\mathrm{\lambda }}\right)$ . The maximum particle velocity is equal to four times the wave velocity if